
| Accueil site | Tableur | Programmation | Outils XML | Tic en stock | Téléchargement | Informations |

|
|||||||
|
 Algorithmique |
| |||||
|
Soit f une fonction définie au moins sur l'intervalle [a ; b].
Dans cet intervalle {a ; b], on recherche une solution, si elle existe, de l'équation : f(x) = 0. Recherche par balayage On peut diviser l'intervalle [a ; b] en N intervalles de même longueur et parcourir [a ; b] par pas de longueur ces intervalles en calculant l'image par f de l'extrémité de chacun des N intervalles. 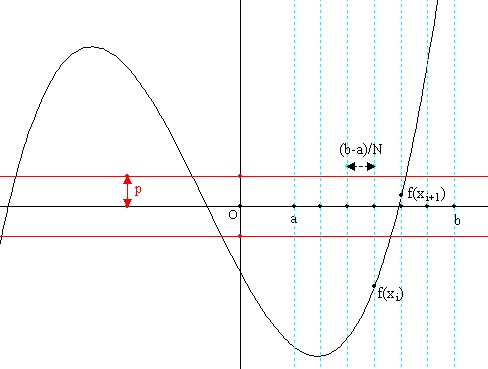 On trouve une solution de l'équation f(x) = 0 dès que la valeur absolue d'une image est plus petite qu'une valeur p donnée (1/10, 1/100, 1/1000 ...). La précision d'une solution dépend de la fonction f, du nombre p ainsi que du nombre N d'intervalles (que l'on peut prendre grand). Algorithme avec Algobox Voici un exemple d'algorithme (qui utilise la structure TANT QUE ... FAIRE pour le traitement et une structure SI .. ALORS pour l'affichage) et qui arrête le balayage dès qu'une solution a été trouvée ou que la valeur testée est supérieure à b. La définition de la fonction doit se faire dans l'onglet Utiliser une fonction numérique en bas de la fenêtre du logiciel en cochant la case Utiliser une fonction. On écrira l'expression de la fonction en utilisant la syntaxe d'Algobox, par exemple pour définir la fonction f telle que f(x) = x3 + x2 - 3x - 1, on écrira : pow(x,3)+pow(x,2)-3*x-1. Le nom de la fonction est F1 et dans le programme, l'image d'un nombre a par la fonction F1 s'écrira : F1(a). 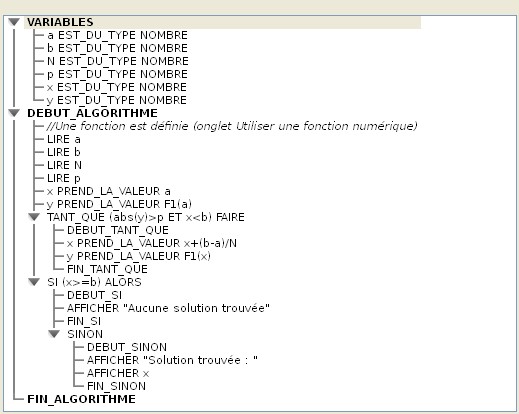 Télécharger le fichier Algobox de ce premier exemple. Remarques Dans cet algorithme, si le nombre d'intervalles est trop petit, la précision sera limitée, s'il est trop grand la durée du traitement peut être importante. Ce nombre N d'intervalles peut être fixé dans l'algorithme au lieu de le faire saisir. Par exemple, avec f(x) = x3 + x2 - 3x - 1 et en prenant le nombre d'intervalles égal à 100000, on peut avoir une solution x0 sur l'intervalle [0 ; 2] telle que |f(x0)| < 0.0001 en quelques secondes. La précision sur la valeur de la solution x0 trouvée est de l'ordre de 0.00001. Cet algorithme n'est pas très performant. En revanche il ne produit pas d'erreur si la fonction donnée ne s'annule pas sur l'intervalle donné [a ; b]. |
||||||