Dossier algorithmique

Toutefois on se limitera, ici, au cas où a et b sont des entiers naturels.

Le but de cet exercice est de trouver la fraction irréductible d'une fraction donnée.

Au préalable, on demandera aux élèves de montrer que :
- si d divise a et b alors d divise a - b.
Ceci étant démontré, on peut leur demander d'appliquer cette propriété à un ou plusieurs exemples.
Prenons 12 et 18, on obtient sucessivement :

	12 et 18
	12 et 6	<-- (18 - 12)
(12 - 6) -->	6 et 6

L'algorithme utilisera cette méthode. Deux entiers étant donnés :
- on calcule leur différence
- on remplace le plus grand des deux par cette différence
- on recommence jusqu'à ce que les deux nombres soient égaux.
C'est alors le pgcd des deux entiers, on les divise par ce pgcd pour obtenir la fraction irréductible.

Si on recommence le traitement une fois, la différence est nulle. On peut utiliser cette propriété pour arrêter le traitement et obtenir le pgcd.
Il faudra donc mémoriser la dernière différence non nulle avant d'effectuer la suivante.

Algorithme simple
Avec Algobox, voici un exemple d'algorithme qui ne tient pas compte de données éventuellement incorrectes entrées par l'utilisateur :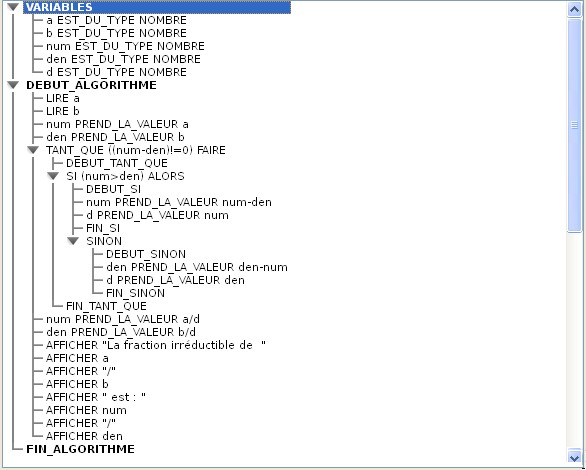

Télécharger le fichier Algobox de ce premier exemple.

Remarques :
La syntaxe d'Algobox impose de noter dans les conditions logiques :
égal par ==
différent par !=
Par exemple pour signifier : (num- den) différent de 0, on écrira : (num - den)!=0
Les 8 dernières lignes de l'algorithme ci-dessus ne sont destinées qu'à un affichage complet du résultat sur une seule ligne. On peut réduire cet affichage au strict minimum. On peut aussi déclarer une variable supplémentaire de type chaîne pour composer un message avec du texte et des valeurs numériques préalablement converties en texte (avec l'instruction nb.toString() où nb est de type nombre).
Par exemple :
mes = "La fraction irréductible de " +a.toString()+"/"+b.toString()+" est "+num.toString()+"/"+den.toString()
AFFICHER mes

Algorithme plus sophistiqué
L'utilisateur, s'il n'est pas averti, peut entrer des données qui ne sont pas prises en charge dans le premier algorithme : boucle infinie si a = 0 ou b = 0, division par zéro si a = 0 et b = 0, division par zéro si a = b.
Il faut donc compléter l'algorithme précédent pour éviter ces cas particuliers :

Télécharger le fichier Algobox de ce deuxième exemple.