
| Accueil site | Tableur | Programmation | Outils XML | Tic en stock | Téléchargement | Informations |

|
|||||||
|
 Algorithmique |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Jeu du lièvre et de la tortue Il s'agit pour le lièvre et la tortue de parcourir un trajet de 6 cases. Pour cela on lance au maximum 6 fois un dé. Le lièvre et la tortue avancent de la manière suivante : - si le 6 sort au cours d'un des 6 lancers, alors le lièvre avance de 6 cases ; - sinon la tortue avance d'une case à chaque lancer. La question est de savoir si le jeu est équitable. On peut donc réaliser un petit programme qui simule ce jeu. On utilisera la fonction randrange() de la bibliothèque random de Python. La première ligne du programme importera donc la fonction de cette bibliothèque : from random import randrange On peut également utiliser une liste, nommée ici tirage, pour mémoriser les différents lancers de dé. Ce n'est pas indispensable mais cette liste permet d'afficher pour chaque partie les lancers successifs (au moins quand le nombre de parties demandées est inférieur à un certain nombre, fixé ici à 20) 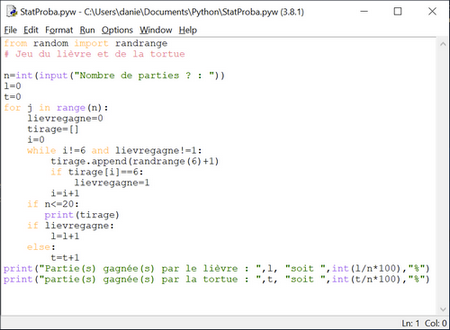 Télécharger ce programme pour Python. En l'exécutant, on obtient par exemple : 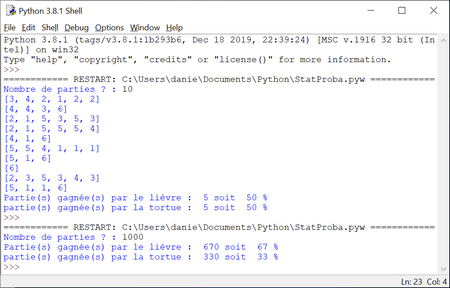 Remarque : Dans le programme précédent, on peut avantageusement remplacer int(l:n*100) par format(l/n*100,",") pour avoir un ou deux chiffres après la virgule. Pistes d'exploitation de ce jeu On s'aperçoit que lorsque le nombre de parties est grand (1000, 2000, ....10000,...) le nombre de parties gagnées par le lièvre est proche de 66% et celui de la tortue 33%. Pourquoi ? Soient :
Pour évaluer la probabilité P(B) de l'évènement B, on peut procéder par différence : P(B)=1 - P(A) Mais on peut aussi calculer directement P(B) sans connaître P(A). On peut demander aux élèves de montrer que : Prolongement Peut-on rendre ce jeu plus équitable ? Par exemple en modifiant le nombre de lancers de chaque partie. On peut faire une étude expérimentale en modifiant légèrement le programme précédent. On introduit une nouvelle variable,ici nbl, pour le nombre de lancers : 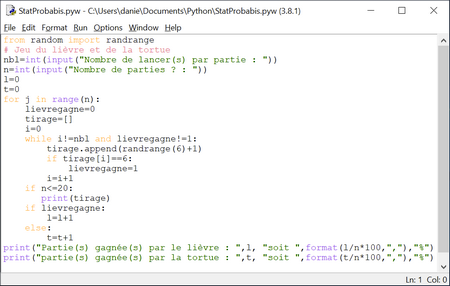 Télécharger ce programme pour Python. Quel est donc le nombre de lancers qui rend plus équitable ce jeu ? Calculer les probabilité des deux évènements A et B pour ce nombre de lancers. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||