
| Accueil site | Tableur | Programmation | Outils XML | Tic en stock | Téléchargement | Informations |

|
|||||||
|
 Algorithmique |
| |||||
|
Soit f une fonction définie au moins sur l'intervalle [a ; b].
On veut savoir (sans utiliser la notion de dérivée) si cette fonction est monotone sur [a ; b]. Pour cela, on peut diviser l'intervalle [a ; b] en N intervalles de même longueur et comparer le signe de f(b) - f(a) avec le signe de la différence des images des extrémités de chaque intervalle. Dès que les signes sont contraires, on sait alors que la fonction n'est pas monotone sur l'intervalle [a ; b]. En revanche dans le cas contraire, on ne peut pas être certain que la fonction est monotone. En effet, il est possible que sur un ou plusieurs des N intervalles la fonction change deux fois de sens mais que l'intervalle soit trop grand pour détecter ce changement. Pour minimiser ce risque on pourra prendre un nombre important d'intervalles. Avec Algobox La définition de la fonction à étudier doit se faire dans l'onglet Utiliser une fonction numérique en bas de la fenêtre du logiciel. Il faut commencer par cocher la case Utiliser une fonction.  Dans cet onglet, la partie de droite, munie d'un ascenseur, donne les indications nécessaires sur la syntaxe à utiliser et les quelques fonctions de base disponibles. Ainsi pour définir la fonction f(x) = x² + 1, on écrira pow(x,2)+1 et le nom de la fonction est F1. Dans le programme, l'image d'un nombre a par la fonction F1 s'écrira : F1(a). Algorithme simple Voici un premier exemple d'algorithme (qui utilise la structure Si ... Alors) et qui arrête le balayage des intervalles dès que les signes sont contraires : 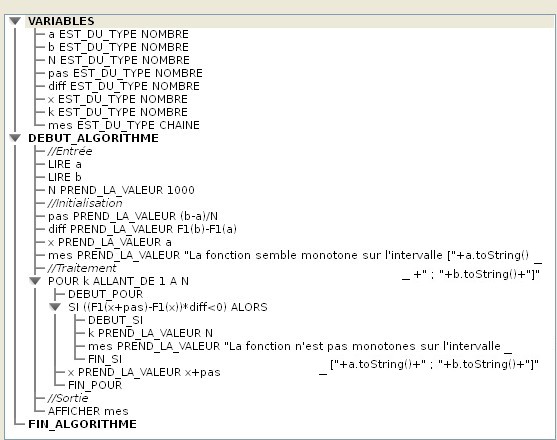 Télécharger le fichier Algobox de ce premier exemple. Remarques Dans cet algorithme, le test des signes est fait avec le produit (F1(b)-F1(a))*(F1(x+pas)-F1(x)), ce qui introduit une contrainte supplémentaire car si F1(a) = F1(b) la fonction est déclarée systématiquement comme semblant être monotone (le balayage des N intervalles n'est pas fait). Il faut donc s'assurer au préalable que ce n'est pas le cas. Pour arrêter la boucle dès que les signes sont contraires, on affecte la valeur N à la variable k. Algorithme plus élaboré Il détecte le problème précédent et le traitement se fait avec une structure TANT QUE ... FAIRE. Il permet aussi d'afficher la courbe représentative de la fonction sur l'intervalle [a ; b]. 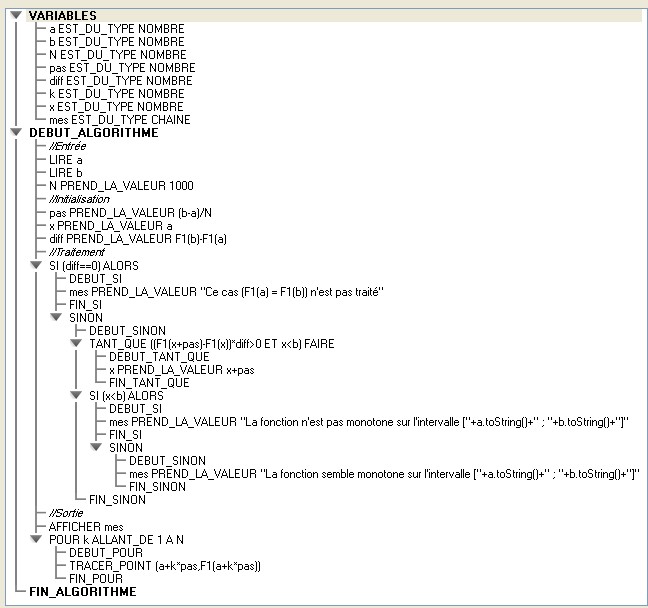 Télécharger le fichier Algobox de ce deuxième exemple. Remarques En début de traitement a été ajoutée une structure SI ... ALORS ... SINON pour éliminer le cas où F1(a) = F1(b). Une boucle de compeur k permet de tracer les N points de coordonnées (x, F1(x)) avec x =a+k*pas. C'est l'instruction TRACER_POINT qui dessine chaque point dans le repère orthogonal choisi. Pour ajouter cet instruction au code et choisir le repère, il faut cliquer sur l'onglet Dessiner dans un repère puis cocher la case Utiliser un repère.  Un clic sur le bouton Ajouter TRACER_POINT affiche une boîte de dialogue pour saisir les coordonnées du point à tracer puis ajoute l'instruction au code. Le repère choisi (ici orthonormal) apparaît automatiquement à l'éxécution du programme : 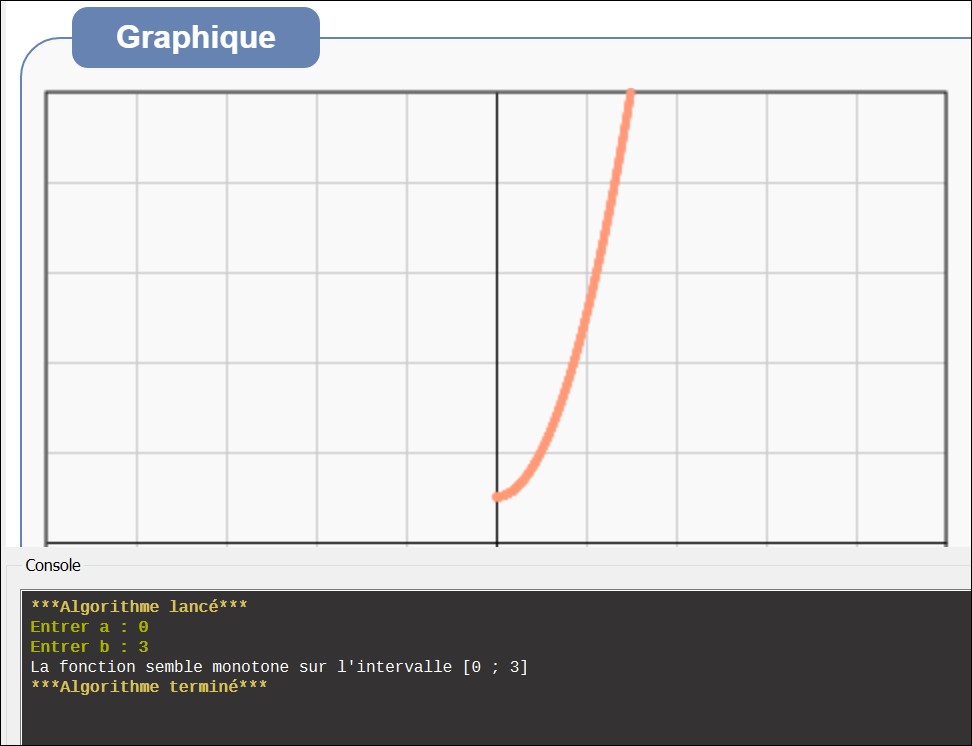 |
||||||