Dossier algorithmique

On veut obtenir la figure suivante :

On utilise la procédure FloconCentre (voir la partie Initiation, Exemple avec LOGO) après avoir avancé d'une certaine longueur (à calculer) à partir de l'origine du repère de manière à ce que chaque flocon n'aie qu'un seul point commun avec ses voisins.
Dans un premier temps on veut dessiner 9 flocons de côté 10 comme ci-dessus. On demande aux élèves d'écrire l'algorithme pour cette figure.

' Position initiale (celle par défaut : l'origine du repère)
' Figure
REPETER 9 fois
Avancer d'une longueur à calculer
Tracer un flocon de côté 10
Reculer de la même longueur que celle avancée
Tourner d'un angle égal à 360/9
FIN REPETE

Il est nécessaire de faire une étude géométrique pour calculer la longueur entre l'origine du repère et le centre d'un flocon.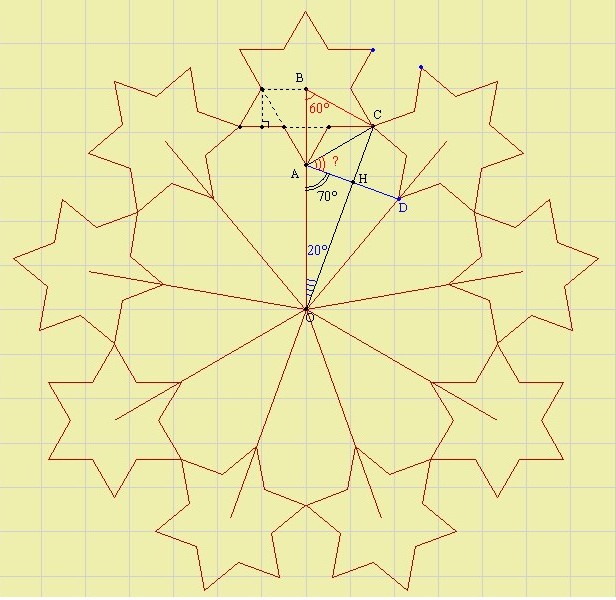

Pour 9 flocons de côté 10 :

Les longueurs OA et OD étant égales et

, justifier la mesure de l'angle

Exprimer la mesure de l'angle

en fonction de celle de

puis calculer

Le triangle ABC étant isocèle, calculer l'angle

Nature du triangle ABC ?

Exprimer la mesure de l'angle

en fonction de celle de

puis calculer

Calculer AB (à l'aide de la longueur du côté du flocon, voir la partie initiation LOGO)

Exprimer cos

en fonction de AH et AC, en déduire AH.

Exprimer sin

en fonction de AH et OA, en déduire OA.

Calculer OB

On a :

= 360°/9 = 40°. Le triangle AOD est isocèle et (AH) est aussi bissectrice, donc

= 20°.

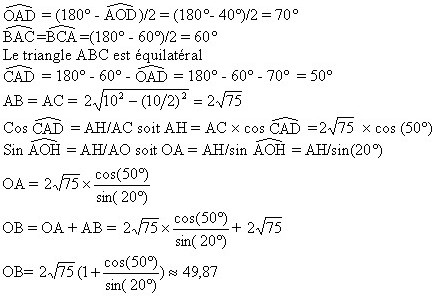Le programme LOGO pour cette figure est donc :
REPETE 9
AV 2*Racine(75)*(1+cosinus(50)/sinus(20))
FloconCentre :10
LC
RE 2*Racine(75)*(1+cosinus(50)/sinus(20))
BC
TD 40
FIN REPETE
CT

Pour n flocons de côté a :

Calculer les angles

en fonction de n.

Calculer AB en fonction de la longueur a du côté du flocon (voir la partie initiation LOGO)

Calculer AH.

Calculer OA.

Calculer OB

Les angles étant exprimés en degrés, on a :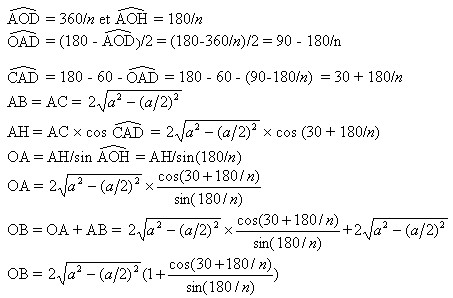

Maintenant on va créer des procédures pour passer en paramètres le nombre de flocons et la taille d'un côté.

Une procédure pour avancer de la position initiale au centre d'un flocon
Pour AllerFleurFlocon : long : n
AV 2*Racine(:long^2-(:long/2)^2)*(1+Cosinus(30+180/:n)/Sinus(180/:n))
Fin Pour

Une procédure pour reculer du centre d'un flocon à la position initiale
Pour RetourFleurFlocon :long :n
RE 2* Racine(:long^2-(:long/2)^2)*(1+Cosinus(30+180/:n)/Sinus(180/:n))
Fin Pour

Une procédure qui appelle toutes les autres :
Pour FleurFlocon :long :n
REPETE :n
AllerFleurFlocon :long :n
FloconCentre :long
LC
RetourFleurFlocon :long :n
BC
TD :360/:n
FIN REPETE
Fin Pour

La figure avec 9 flocons de côté 10 s'obtient maintenant avec une seule ligne de programme :
FleurFlocon :10 :9 CT

Mais on peut maintenant tracer les figures en faisant varier le nombre et/ou la taille des flocons; par exemple :
FleurFlocon :8 :12 CT
Essayer pour n = 1, n = 2, n = 3, ...