
| Accueil site | Tableur | Programmation | Outils XML | Tic en stock | Téléchargement | Informations |

|
|||||||
|
 Algorithmique |
| |||||
|
Soit f une fonction définie au moins sur l'intervalle [a ; b].
Dans cet intervalle {a ; b], on recherche une solution, si elle existe, de l'équation : f(x) = 0. Recherche par dichotomie Dans l'exemple ci-dessous, [a ; b] est l'intervalle où se trouve la solution cherchée. 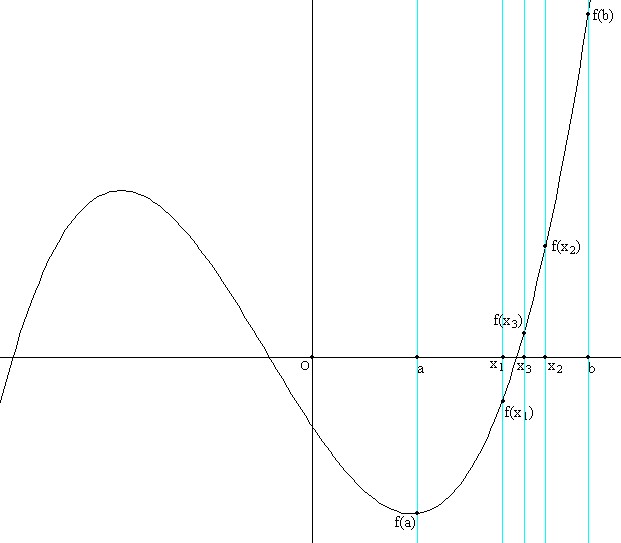 x1 milieu de |a ; b] est tel que f(x1) et f(a) sont de même signe donc [x1 ; b] est l'intervalle où se situe la solution. x2 milieu de [x1 ; b] est tel que f(x2) et f(x1) sont de signe contraire donc [x1 ; x2] est l'intervalle où se trouve la solution. x3 milieu de [x1 ; x2] est tel que f(x3) et f(x1) sont de signe contraire donc x1 ; x3] est l'intervalle où se situe la solution, etc. Sur cet exemple, la fonction est croissante : on peut vérifier que la méthode de sélection des intervalles successifs est la même lorsque la fonction est décroissante. Algorithme simple avec Algobox Dans ce premier algorithme une structure SI ... ALORS ... SINON emboîtée dans une simple boucle avec compteur permet de trouver une solution lorsqu'il y en a une. 50 itérations sont suffisantes pour avoir une précision supérieure ou égale à d/250 où d est l'amplitude de l'intervalle [a ; b]. En effet, on divise par deux à chaque itération l'amplitude de l'intervalle où se trouve la solution. Une structure SI ... ALORS interne à la boucle permet de choisir la bonne extrémité pour l'intervalle suivant. La définition de la fonction doit se faire dans l'onglet Utiliser une fonction numérique en bas de la fenêtre du logiciel en cochant la case Utiliser une fonction. On écrira l'expression de la fonction en utilisant la syntaxe d'Algobox, par exemple pour définir la fonction f telle que f(x) = x3 + x2 -3x - 1, on écrira : pow(x,3)+pow(x,2)-3*x-1. Le nom de la fonction est F1 et dans le programme, l'image d'un nombre a par la fonction F1 s'écrira : F1(a). 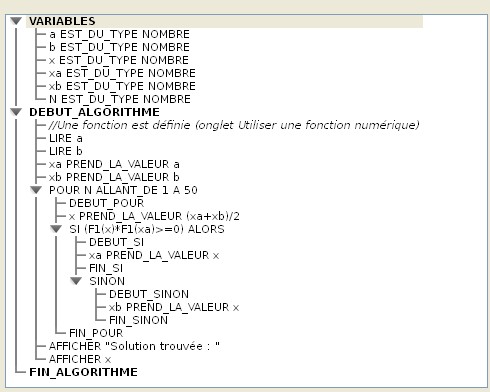 Télécharger le fichier Algobox de ce premier exemple. Remarques Dans cet algorithme, si la fonction f ne s'annule pas dans l'intervalle donné ou que f(a) et f(b) ne sont pas de signe contraire, le programme donne une solution erronée. En effet, l'algorithme est fondé sur cette hypothèse. Par exemple, sur l'intervalle [-1 ; 1] l'équation : 1 + x² = 0 donnera une solution alors qu'il n'en existe pas et l'équation -1 + x² = 0 donnera une solution erronée sur l'intervalle [-2 ; 2] et la bonne solution sur l'intervalle [0.5 ; 2]. Mais d'autres erreurs sont engendrées par la comparaison des signes de f(x) et f(a) à chaque itération. En effet, dans la condition (F1(x)*F1(a)>=0) de la structure Si ... ALORS, les cas F1(x) = 0 et F1(a) = 0 ne sont pas traités. Par exemple, les équations suivantes n'auront pas de solution valide sur [0 ; 1] : x² = 0 |x| = 0 ici, bien que ces deux équations possèdent une solution et que les fonctions définies par f(x) = x² et g(x) = |x| soient croissantes sur cet intervalle, on a ici le cas où f(0)=0 et g(0) = 0. F1(x) = 0 est le cas où le milieu d'un intervalle est exactement une solution. Par exemple si on cherche une solution de l'équation : -1 + x² sur l'intervalle [0 ; 2], une solution est justement x = 1 (le milieu de l'intervalle) et l'algorithme précédent continue le traitement avec des intervalles qui ne contiennent plus la solution. On doit donc vérifier au préalable l'allure de la courbe représentative de la fonction choisie par exemple avec un logiciel traceur de courbe et déterminer judicieusement l'intervalle approprié. Le logiciel libre MathGraph32 (téléchargement gratuit) est un logiciel de géométrie dynamique qui est aussi un excellent traceur de courbe qui apporte une aide précieuse. Algorithme amélioré Cet algorithme gère les cas où f(x) = 0 et f(a) = 0. Il précise aussi si la solution trouvée est exacte ou approchée..  Télécharger le fichier Algobox de ce premier exemple. Remarque Avec cet algorithme, on doit toujours veiller à ce que la fonction s'annule dans l'intervalle donné et que f(a) et f(b) soient de signe contraire. Algorithme permettant de choisir la précision avec Algobox Voici un exemple d'algorithme qui remplace la boucle avec compteur par une structure TANT QUE ... FAIRE. On arrête le traitement quand l'intervalle contenant la solution a une amplitude inférieure à une précision donnée (1/10, 1:100, 1/1000 ...), ce qui assure d'avoir une solution de l'équation f(x) = 0 avec au moins cette précision.  Télécharger le fichier Algobox de ce deuxième exemple. Remarques Comme dans les exemples précédents, si la fonction n'a pas de zéro dans l'intervalle [a ; b] ou que f(a) et f(b) ne sont pas de signe contraire, le programme donne une solution erronée. En revanche, si ces conditions sont vérifiées, cet algorithme est très performant. Pour s'en rendre compte on peut ajouter une variable, par exemple N, permettant de compter le nombre d'itérations nécessaires pour une précision donnée. Il faut donc ajouter une variable : N EST DU_TYPE NOMBRE Puis ajouter une ligne en première ou dernière position dans la structure TANT QUE ... FAIRE : N PREND_LA_VALEUR N+1 Et enfin faire afficher la variable N en fin d'algorithme (ajouter un retour à la ligne dans l'affichage de x) : AFFICHER N Avec la fonction f telle que f(x) = x3 + x2 -3x - 1, une recherche d'une solution de l'équation f(x) = 0 sur l'intervalle [0 ; 2] se fait en 15 itérations pour une précision de 0.0001. Télécharger le fichier Algobox de l'exemple modifié comme ci-dessus. Algorithme plus complet avec Algobox Il s'agit de modifier l'algorithme précédent en tentant de remédier au cas où l'utilisateur rentre des données non appropriées. On peut, par exemple, vérifier pour un intervalle [a ; b] donné que f(a) et f(b) sont de signe contraire et ne lancer le traitement que dans ce cas. On ajoute une structure SI ... ALORS ... SINON et on y introduit tout le traitement précédent à partir de la structure TANT QUE ... FAIRE. 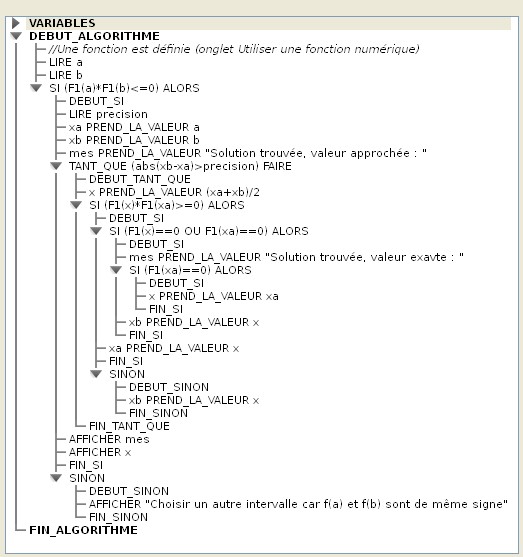 Télécharger le fichier Algobox de ce nouvel exemple. Remarque On peut également faire cette vérification de la même manière avec le premier algorithme amélioré. |
||||||