| Accueil site | Tableur | Programmation | Outils XML | Tic en stock | Téléchargement | Informations |
|
|
|||||||
|
 Algorithmique |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
L'algorithme de Héron d'Alexandrie Il s'agit de calculer une valeur approchée de  (méthode que l'on peut généraliser à tout entier naturel n). La solution de Héron d'Alexandrie peut se formuler simplement de la manière suivante : Sachant que est le côté d'un carré d'aire égale à 2, on considère un rectangle de longueur 2 et de largeur 1 puis par étapes successives on retaille le rectangle en utilisant toujours la même méthode pour obtenir un carré tout en gardant son aire constante. La méthode utilisée consiste à prendre à chaque fois comme nouvelle longueur la moyenne des dimensions du rectangle précédent. Première étape Encadrement de  par des décimaux à une décimale Deuxième étape On demande aux élèves de calculer à la main (calcul sur les fractions) au moins les deux premières étapes :
Troisième étape On demande aux élèves d'utiliser cet algorithme avec un tableur. On peut les laisser créer leur propre feuille de calcul avec 3 colonnes (une pour noter les étapes, les deux autres pour calculer respectivement la longueur et la largeur des rectangles successifs) ou utiliser un fichier préparé (télécharger le fichier Excel ou Calc).  Dans un premier temps, les formules sont très simples si on ne s'intéresse qu'à (2 peut alors être mis en constante dans les formules pour calculer la largeur). La recopie des formules se fait alors sans problème. On fera remarquer aux élèves que la recopie est en réalité une boucle (on fait le même calcul p fois, p étant le numéro de l'étape finale). En pratique, on s'apercevra que la précision d'un tableur ne permet pas de dépasser la sixième étape (limite de 15 chiffres). On pourra comparer à la précision donnée par plusieurs fractions (577/408, 665857/470832, ...) Dans un deuxième temps, on peut généraliser à la racine d'un entier naturel n quelconque (en entrant dans une cellule la valeur de n). Le contenu de cette cellule est alors utilisé dans la formule de calcul des largeurs successives en références absolues (télécharger les fichiers complétés pour Excel ou Calc). 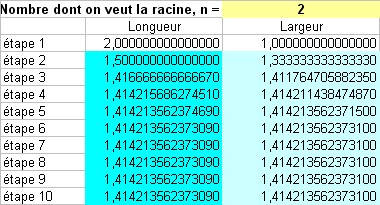 Quatrième étape On voit avec le tableur que 10 étapes sont suffisantes pour tout entier naturel inférieur à 1000. On se limitera à ce cas (n < 1000). On demande aux élèves (en les aidant) de formaliser collectivement l'algorithme pour calculer la racine Variables utilisées a (largeur) b (longueur) d'un tel entier. L'observation des formules recopiées doit mener à l'idée d'une boucle. n (nombre dont on veut la racine) p (compteur pour la boucle) Entrée Saisir n Traitement Initialisation (cette partie correspond à la première ligne des calculs dans le tableur) b prend la valeur n a prend la valeur 1 Début boucle (cette partie correspond à la recopie des formules dans le tableur) Pour p variant de 1 à 10 faire :
Fin Boucle Sortie Affichage b Il est nécessaire d'expliquer les affectations en particulier b prend la valeur (a + b)/2 (traduit dans certains langages par b = (a + b)/2, ce qui n'est pas très explicite). b prend la valeur (a + b)/2 signifie que l'on affecte à la variable b le résultat du calcul (a + b)/2 (le calcul étant effectué avec la valeur actuelle de b avant l'affectation à b de sa nouvelle valeur, ce qui se comprend si on pense que b est la valeur contenue dans des cellules de mémoire qui doivent être lues puis écrites). On voit également que l'on peut modifier et rendre plus performant cet algorithme :
Variables utilisées b (longueur) n (nombre dont on veut la racine) p (compteur pour la boucle) Entrée Saisir n Traitement b prend la valeur n Pour p variant de 1 à 10 faire :
Sortie Affichage de b Mais si on saisit n = 0, Que se passe-t-il ? L'algorithme explicité ci-dessus pose un problème : on effectue une division par zéro. Il va falloir éliminer ce cas par un test de la valeur affectée à la variable n. D'où la troisième version de l'algorithme avec une « structure alternative ». Variables utilisées b (longueur) n (nombre dont on veut la racine) p (compteur pour la boucle) Entrée Saisir n Traitement Structure alternative Si n = 0 alors
Fin structure alternative Sortie Affichage de b Ce nouvel algorithme donne lieu à une variante de l'algorithme précédent que l'on peut utiliser avec un tableur (télécharger les fichiers Excel ou Calc à compléter par les élèves ou les fichiers déjà complétés Excel ou Calc). 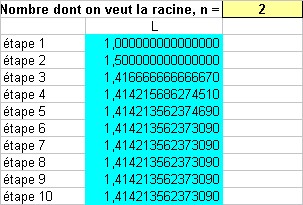 Á l'étape 1, une fonction Si permet de tester si n=0. Cinquième étape On peut traduire ce dernier algorithme avec un logiciel d'initiation à l'algorithme comme Algobox. 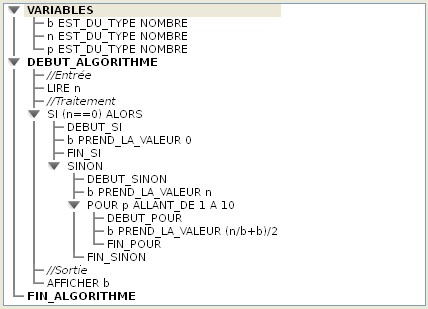 Télécharger le fichier complété Algobox (le signe = = est le test d'égalité dans une condition). On peut également très facilement traduire cet algorithme avec le langage (Visual Basic) intégré à Excel ou avec le langage (OppenOffice Basic) intégré à Calc (voir plus bas). Dans une feuille de calcul d'Excel, il faut réserver une cellule (par exemple C10) pour la saisie de n (nombre dont on veut la racine), une autre pour l'affichage du résultat (par exemple C12) comme ci-dessous.  Puis il faut créer un bouton de commande (avec la barre Visual Basic), nommé par défaut CommandButton1 (voir les documents ressources ci-dessous). On implémente le code suivant dans la fenêtre de code (accès par Alt+ F11) dans la procédure évènementielle Click du bouton. Un clic sur le bouton affiche le résultat. Private Sub CommandButton1_Click() Dim n As Double Dim b As Double Dim p As Byte n = Cells(10, 3).Value If n = 0 Then
Cells(12, 3).Value = b End Sub Remarques :
Pour p variant de 1 à 10 faire
Tant que p<10 faire
For p = 1 to 10
Do While p<10
Ressources - Dessiner l'interface - Environnement de développement - Compléments pour Office 2007 - Régler le niveau de sécurité - Télécharger le fichier complété de cet exemple Pour Calc, la présentation de la feuille de calcul est identique à celle d'Excel et le programme semblable en dehors de l'accès aux objets de la feuille de calcul (déclaration des variables objets) et des références de cellule (numéro de colonne, numéro de ligne) avec les index commençant à 0 (voir les documents ressources) : REM ***** BASIC ***** Sub RacineCarree Dim LesFeuilles as Object Dim PremiereFeuille as Object Dim Cellule as Object Dim n as double Dim b as double Dim p as integer LesFeuilles = ThisComponent.Sheets PremiereFeuille = LesFeuilles.GetbyName("Feuil1") Cellule = PremiereFeuille.GetCellByPosition(2,9) n = Cellule.Value If n = 0 Then b = 0 Else b = n For p = 1 To 10 b = (n / b + b) / 2 Next p End If Cellule = PremiereFeuille.GetCellByPosition(2,11) Cellule.Value = b End Sub Mêmes remarques que pour Excel.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1,333